彩世(あやせ)のトップハット ビームシェイパー テクノロジー
特徴と活用利点
- レーザービームを均一な強度分布(トップハットプロファイル)に変換し、入射したガウシアンビームなどを中心からエッジまで安定した強度を持つビームを生成できることから、高精度かつ均一な結果を得ることができます。
- 微細さ、精密さを求められる検査や加工において、均一なビームプロファイルを提供。
- 非接触操作でビーム整形ができるため、光学要素に物理的なダメージを与えることがない。
- 可視光から赤外線まで、広い波長範囲に対応できるため多岐に渡る用途に活用できる。
- レーザービームの直径や形状に応じてカスタマイズが可能である。
- コストカット、工程数カット、性能向上が期待できる。
ラインビームシェイパー/ LINE Beam Shaper(LBS)
彩世(あやせ)のラインレーザーモジュール・LINEMANシリーズに用いられている、独自に開発したラインビームシェイパー(LBS)は、パウエルレンズを使った場合に比べ、均一なライン強度が得られます。また、このレンズはモールドプレスで作成する事が可能で特性のバラツキが少なく、その結果得られるラインのバラツキも小さくなります。これらすべての特性を、業界最小クラスのPKGに収めて供給をしています。これらの事を順に説明して行きます。
Good Repeatability
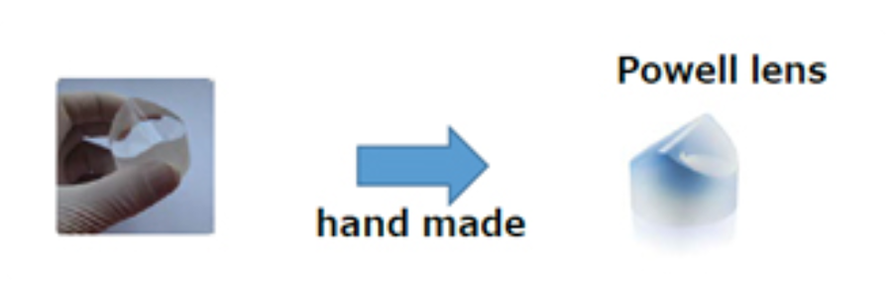
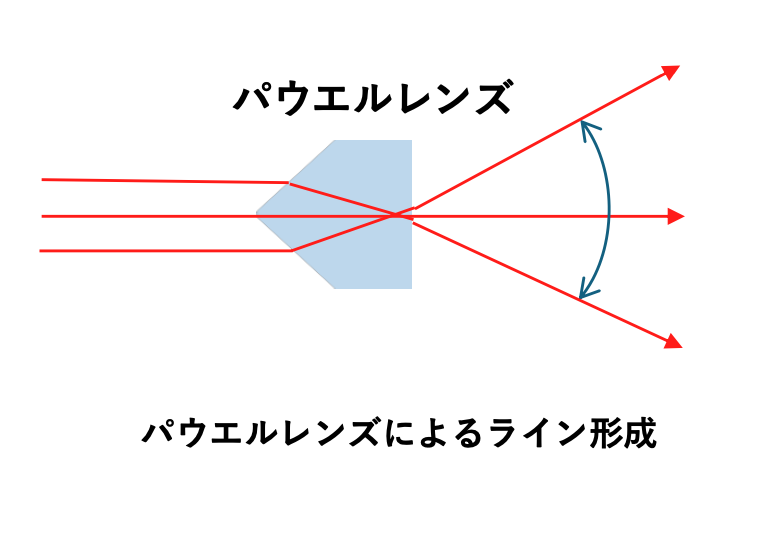
パウエルレンズは、レーザ光の入射側に急峻な突起を持った形状をしており、後述するようにこの突起部分周辺の曲面がビームの均一性に与える影響が大変に大きいですが、この形状を作成するのは人間の手によるポリッシュによっています。そのため人のスキルによるバラツキが出る事なります。

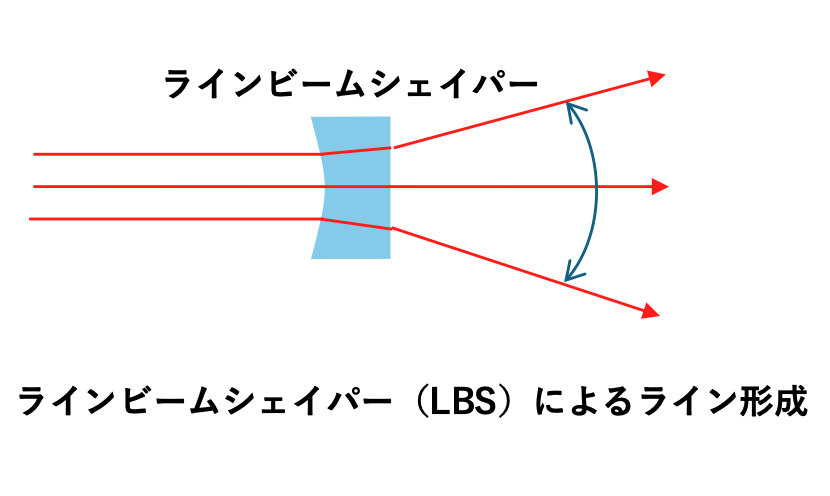
それに対して、弊社のラインビームシェイパー(LBS)は、非常になだらかな曲面のみの形状であり、モールドプレスで作成することが可能です。理論的に均一なビーム強度を得られる形状のレンズを再現性良く作る事が可能となっています。
Good Uniformity
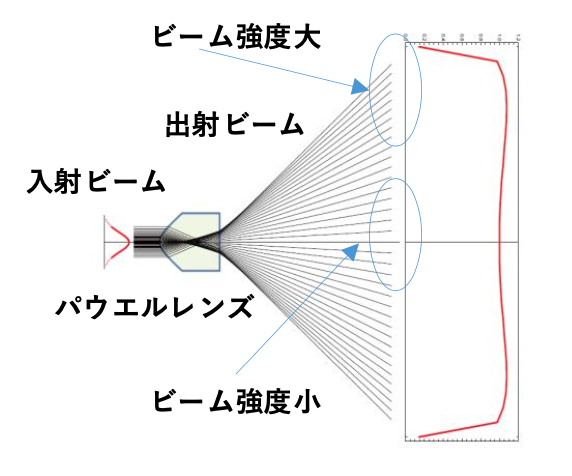
一般的なラインジェネレーターではラインを作るのにパウエルレンズが使われることが普通です。パウエルレンズは、2次のオーダーまでの近似式で形状を決めることが多く、その場合ビーム強度を完全に均一にすることは理論的にも不可能です。
ラインの端側はどうしてもビーム強度が強くなる傾向にあり、一方、両端の強度が強くなるのを抑えようとすると、真ん中が凹む事になります。
左の図は、両端の強度が強くなるのと、真ん中の強度が落ちる事のバランスを取った理論値になりますが、理論上でも均一なビーム強度を得る事が出来ない事が分かります。実際には、この理論値にパウエルレンズの製造上のバラツキ、レーザの発散角のバラツキなどが加わりますので、その結果ビームの均一性は落ちていく事になります。
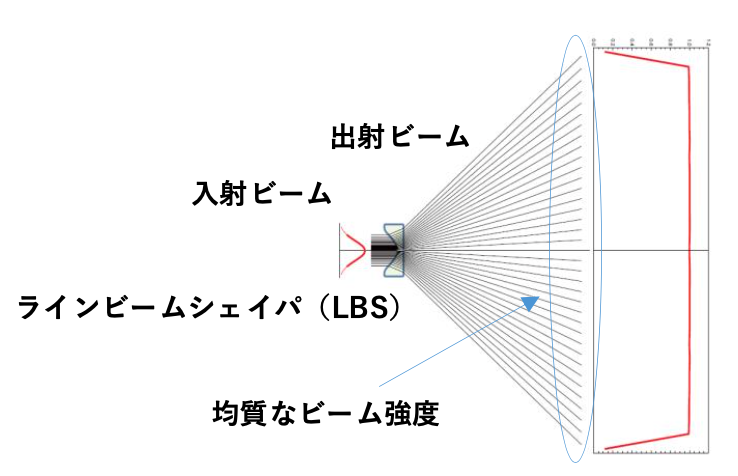
それに対して弊社のラインビームシェイパー(LBS)は、数値積分で近似無しに面の形状を決めることができ、理論値では完全なフラットなビーム強度を得る事が可能です。また、前項で説明しました様に、ラインビームシェイパーの製造上のバラツキは、パウエルレンズに比べて小さく抑えることが可能となっています。
業界最小クラスの小型化を実現 6.5mmパッケージ

弊社では、パッケージの設計と組み立てにも独自のプロセスを使い、業界最小クラスの小型化を実現しています。ラインジェネレーターでは、18mm径程度のパッケージが使われる事が多いですが、彩世(あやせ)では一番小さい物では6.5mmのパッケージにてお客様に提供しております。
従来の組み立てプロセスにとらわれずに小型化を実現させるプロセスを開発し、小型化による熱はけの問題を考慮しながら業界最小のPKGを実現しました。
高出力モジュールにおいてもφ8mmのPKGを採用しており、今後アプリケーションが拡大していく中で、小型化の要望をいち早く取り入れたパッケージ展開をしています。
小さいPKGでありながら、APC回路、デジタルモジュレーションのためのTTLシグナルインプットの回路も内蔵しています。
ラインビームシェイパー(LBS)を用いた ラインレーザーモジュール
<LINEMANモジュール ラインナップ>
-スーパーストレイト・ラインマン
-マルチプル・ラインマン
-ウルトラコンパクト・ラインマン
<オプション>
1アジャスタブル・ホルダー
2APC モジュール
マイクロビームシェイパー/ μ-Beam Shaper(MBS)
マイクロビームシェイパーは、ガウシアンビームを照度均一の正方形状の光ビームに変換する高精度なトップハットビームシェイパーです。正方形の他、円形、長方形への変換、或いはトップハット以外の強度分布への変換も可能です。滑らかな非球面レンズにより特定の波長に制限されない多波長対応が可能です。
この技術は、従来のDOE型(Diffractive Optical Element)のトップハットビームシェイパーの課題とされていた欠点をカバーする、これまでにない優位性の高いトップハットビームシェイパーです。

従来のDOE式との比較優位性
- [高効率] 効率の低下がない。 偽スポットがなく、理論効率が高い。補正、再調整不要
- [多波長] 波長に依存性がない。ひとつの素子で、広い波長範囲の対応が可能
- 耐久性の向上
- トップハットププロファイルの品質向上
- 熱劣化が少ない
- 設計プロセスの効率化
- さらに製造コストの削減ができる
- 複数光源の搭載も可能である
- カスタマイズ可能
このような特徴を持つレーザーモジュール製品はこれまでありませんでした。
アプリケーション例としては、フローサイトメトリ、パーティクルセンサー、レーザーマーキングなど、様々な業界の多種多様な製品に活用されることが期待されています。
マイクロビームシェイパー(MBS)を用いた マイクロレーザーモジュール
<μレーザーモジュール ラインナップ>
-µLINEMAN(ラインビーム)
-µSQUAREMAN(スクエアビーム)
<オプション>
1アジャスタブル・ホルダー
2APC モジュール
*モジュール製品のラインナップ詳細は、Ayase Products トップハットビームシェイパーページをご覧ください。
多波長ALL IN ONEモジュール
弊社独自のマイクロビームシェイパー技術を用い、複数の光源を一括して高品位なトップハットビームに変換することができます。搭載する光源は幅広い半導体レーザーラインナップから選択できます。
光源ごとに光学系を用意する必要がないため、システムの簡素化・省スペース化に大きく貢献します。
【特長】多波長 ALL IN ONEのコンパクトモジュール
- 小型多波長ライトユニット
- サイズ:55×105×55mm(3波長用)
- ライン・トップハット、スクエア・トップハットの選択可能
- 超高品質なビーム特性
- 搭載する半導体光源の選択が可能(最大4波長)
- パソコンからのプラグ&プレイ
- パワーエンハンスユニットをオプションで用意
【アプリケーション例】
- フローサイトメトリー
- レーザー顕微鏡
- DNA解析
- 細胞分析
【光学技術】 Top-hat 変換について
はじめに
私たちは半導体レーザを中心とした光源モジュールなどの製品開発を行っています。以下は、光学、電気、機械などの技術をまとめ上げたものです。ここでは私たちの製品をより理解していただくため、これから製品にまつわる、光学的な技術に関するお話を簡単にご紹介致します。専門用語については、当HPの用語集もご活用ください。
均一照明の重要性

図 1: レフ板(Wikipedia から)
ヒトの視覚は視細胞の感度と瞳孔の大きさを調整して、光の量が多くても少なくてもある程度の対応ができるようになっています。しかし網膜のある部分にある特定の視細胞の感度を調整することはできません。つまり視野の中に明るいところと暗いところが同時にある場合にはその調整機構は役には立ちません。
視野の中で強い明暗がある情景は目が疲れやすく、暗いところにあるものは見えなくなるので、絵画的な演出が目的でないなら、できるだけまんべんなく一様に光が届いていることが望ましいということになります。
均一照明のために現在ではいろいろな手段が考案されています。例えば図-1のレフ板などを見かけることもあると思います。これは反射光を拡散させる作用があります。透過型のものはたとえば1眼レフのホットシューに取り付けるストロボの発光源の窓についています。
拡散板は図-2にあるように基本的には入ってきた光をいろいろな方向に広げる機能があります。
入射光束の強度分布がどんな形になっていたとしても、拡散板を透過したあと、拡散板の正面では強度分布が均一化されていきます。
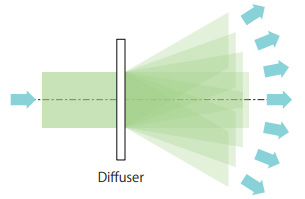
図 2: 拡散板の働き
拡散板による均一化の数値実験
拡散板の機能による均一化を確かめるために数値実験をしてみます。
ある幅の窓に強度が場所ごとに正規分布にバラついた光が入ってくるとします。これは極端な例で、ある場所とそのすぐ隣との光強度が無相関というのはありえないのですが、わかりやすくそうしておきます。
拡散板を透過すると図-3 のように強度分布がずらされていきながら重なることになります。
これがいくつも重なるとどうなるかを計算したのが図-4 です。
図中左のちいさな箱にあるのはそれぞれ数字の回数だけ横ずらしして足したもの、右の図はそれを同時に描いたものです。
台形形状になるため上辺の長さは減っていきますが、その代わりギザギザしたノイズは減っていって平たくなっていくのがわかります。
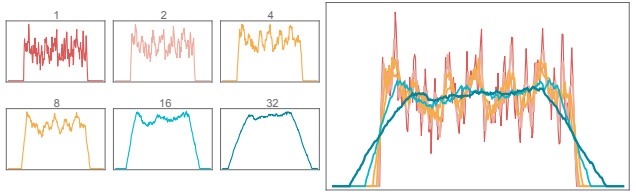
図 3: 拡散板の効果の数値実験
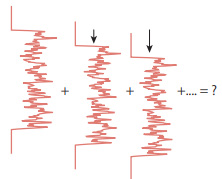
図 4: 数値実験の結果
つまりたくさん重ねるほどノイズは小さくなっていきます(この話が目的ではないので証明は省略します)。
このように拡散板には強度分布を均一化する機能があります。以前はただのすりガラスで、パラメータといえば粗度だけだったものが、最近では微細加工の技術によって拡散方向の制御など、いろいろなパラメータが指定できるようになっています。
また、図-5 のようなライトパイプやフライアイレンズといった素子もあります。これらは拡散板とは違った用途に利用されますが、基本的な原理は上に示した拡散板と同じで、光の強度分布の均一化のための素子です

図 5: 光強度分布を均一化する素子の例
レーザ光の場合
白熱電灯や LED などの光は拡散板やその他の光学素子で光の強度分布を均一化することができます。一方、レーザ光のようにコヒーレンスな光は、白熱電球やLED の光と違って拡散板を通すとスペックル(Speckle)というノイズが出てしまいます
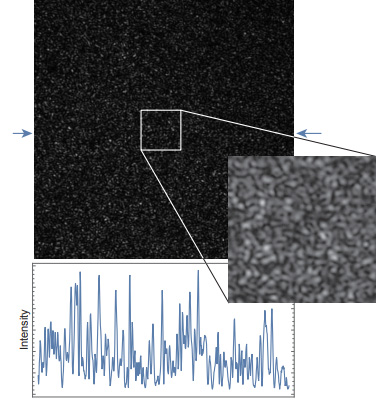
図 6: スペックルの例
図-6 は半導体レーザの光を拡散板に反射させたときの光強度の分布を示したものです。下のグラフは矢印の直線の上の強度分布です。このように細かな粒状のノイズが現れます(これはまた別のところでお話しします)。
光が拡散板のような粗面で反射すると、図-7 のように光路長の異なる光が同じ位置に到達するので、普通の光では均一になるはずですが、レーザではコヒーレンシが高いため干渉が起こって光の強弱が発生します。
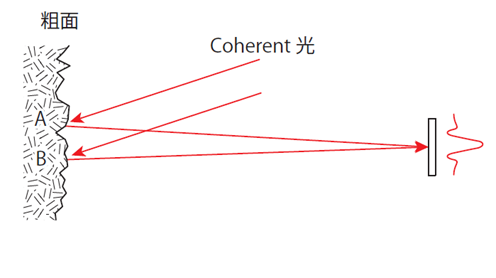
図 7: スペックルの発生
これではとても「均一な照明」とは言えません。つまり、白熱電灯や LED では光の強度分布を重ね合わせることで均一化できたのですが、レーザの光に同じことをするとかえってノイズが増えてしまって、重ね合わせるという手法が使えない、ということになります。
しかしスペックルは干渉の結果なので、干渉が起こらなければスペックルは発生しません。干渉が起こらないようにするには、異なる光路長の光が同じ点に到達しなければいい、ということになります。その上で強度分布が均一になるようにするにはひと工夫が必要です。
アフォーカルなTophat 変換
図-8 にあるレンズをみてください。
これは左から平行光入射して、右へ平行光射出する、いわゆるアフォーカル(Afocal) レンズという、焦点距離無限大のレンズです。図中、細い黒線は光線追跡という計算法で計算した光線の透過の仕方を表しています。それぞれの光線は交わることがなく、したがってレーザ光束の中にこのレンズを入れたとしても(入れる前にスペックルがないなら、入れたことによって)スペックルの発生はないということがわかります。
また、左側に縦を向いた矢印が描いてありますが、これは光線 4 本分の幅を表しています。レンズに入る前左側では矢印の長さはみな同じですが、レンズを透過したあとは矢印の長さが違っていて中央は長く、端に行くほど短くなっています。つまり、光線の密度が入射前後で変わるようなレンズになっています。
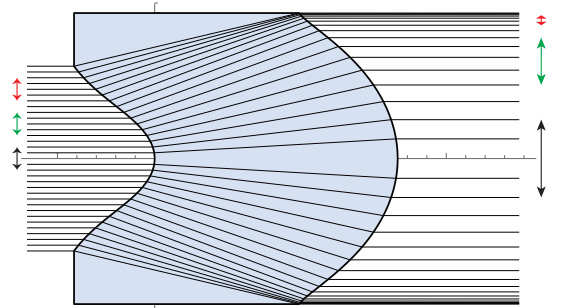
図 8: アフォーカルレンズ
レーザの強度分布
レーザはその発光媒質の大きさに比べるとずっと小さな発光面積になっています。少なくとも出てくる光は小さな一点から出てくるように見えます。また角度分布はLED などに比べるとずっと狭く、ほとんど広がらずに出てきます。
この発光体がほぼ点に見えることと、ほとんど広がらないことから、レーザ光を目で直接覗き込むと、水晶体によって発光点が網膜に結像して、そこにレーザから出てくる光のほぼ全てが集中するため、網膜を焼いてしまう可能性があります。他の光源ではよほど強いものでない限り網膜を焼く心配はないため、レーザにだけ安全基準が設けられています。
またレーザは特定の角度分布を持っているものが多くなっています。それは発光効率を高めるための一つの条件になっているため、レーザの設計上そうある必要があるからです。
ある角度θrad 方向に出る光の強度を I(θ) とすると
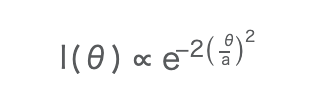
というガウシアンの形になっています。ここでα は広がりの大きさを決める定数で、θ = α の方向へはθ = 0 の方向への強度の 1/e2(≈13%)になるということです。α の値はレーザごとに違っていて、例えば低パワーのHe-Ne レーザではα ≈ 0.5mrad ぐらい、半導体レーザではα ≈ 0.1 ∼ 0.5rad(≈ 8 ∼ 40 °)ぐらいです。典型的な形を図-12に示し
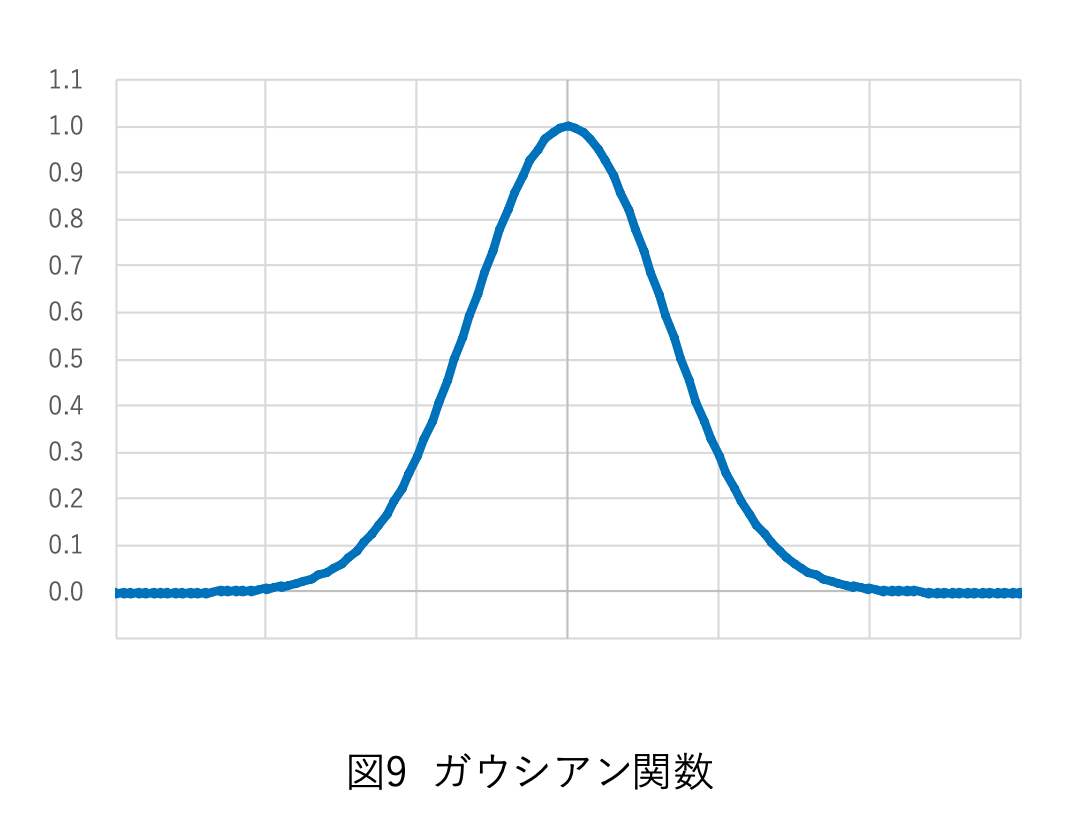
このように広がり方はレーザによっていろいろですが、ほぼすべて(特に低パワーのレーザでは)の角度分布はガウシアンの格好をしています。つまりまんなかは光が強く、外に行くほど弱くなります。
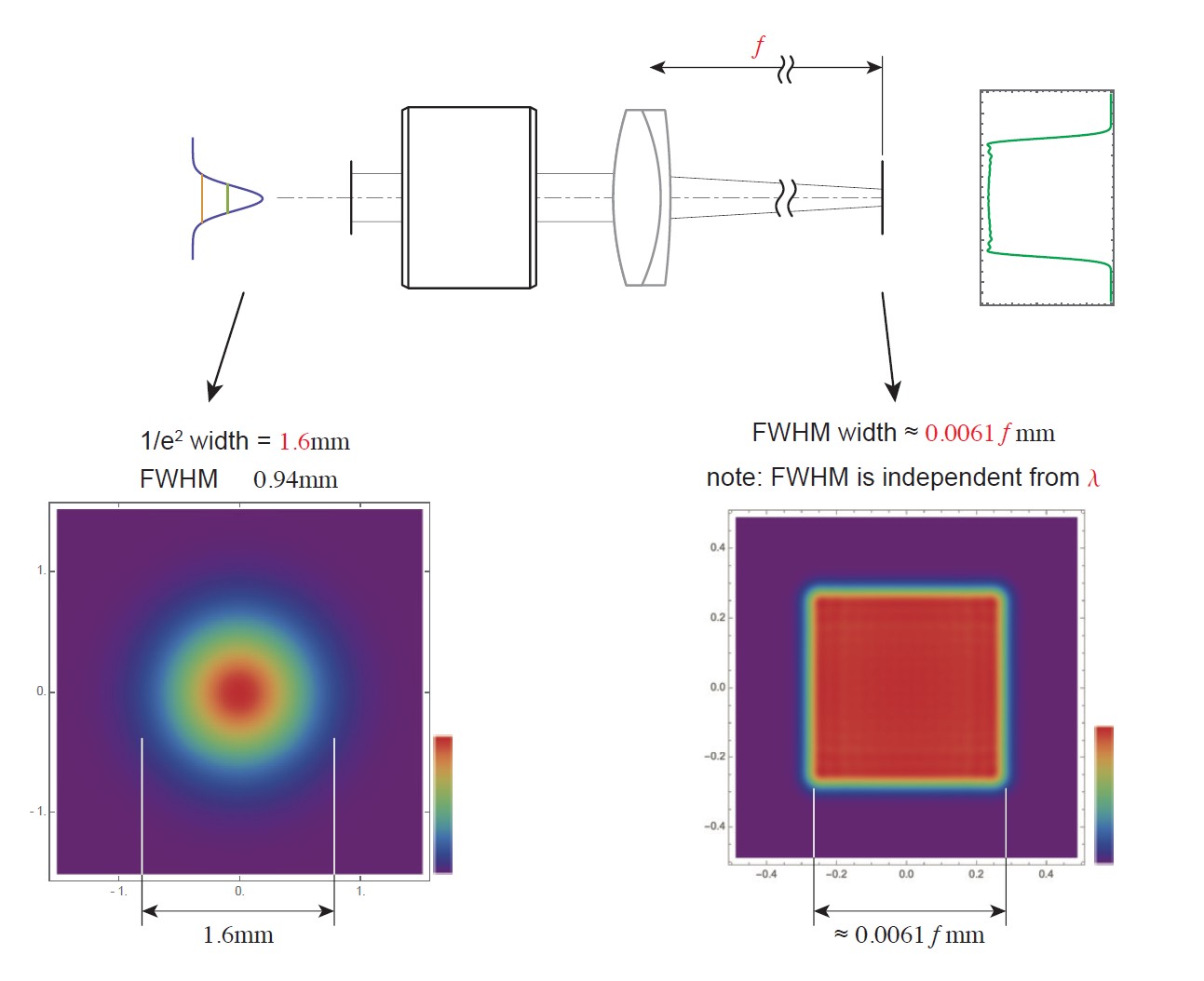
ガウシアン to トップハット変換
もし図-8 のレンズにガウシアンの強度分布を入射させると、均一な強度分布に変換されて出てくるのではないか、と期待できます。
このような均一な強度分布への変換をトップハット(Tophat)変換と言います。トップハットというのは男性用のフォーマルな帽子でいわゆるシルクハットのことです。この帽子のてっぺんが平らで、均一な強度分布の形がこの帽子を横から見た形と似ていて、
直感的に輪郭のイメージが湧くのでこのように呼ばれるようです。このレンズによってレーザ光をスペックルなしで均一な光の強度分布にすることができます。ただもちろんレンズによる光線密度の変化がガウシアンの形とちょうど逆になっている必要があります。また広がりのあるガウシアンではなく、平行光で入射させる必要があります。
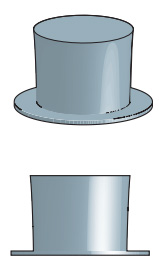
図 10: トップハット
より広い範囲にするために
前節ではアフォーカルな例を示しました。しかしこれではレンズの径よりも広い範囲を照明することはできません。レンズは小さく、照明範囲は広くするほうが望ましいと考えられます。そのためにはどうすればいいか、というのはすぐ思いつきます。つまり図-11 のように光線を扇型にして照明範囲を広げればいいのです。
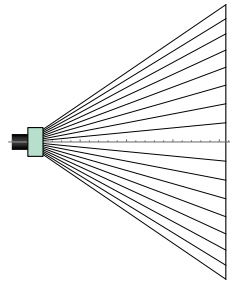
図 11: 照明範囲拡大
ここで一点気をつけなければいけないことがあります。アフォーカルなレンズでは照明対象の平面に光線はすべて垂直に入っていました。ところがこの図のような光学系によると、光線の入射する角度が場所によって違ってきます。そのような場合の光強度というのはどう考えればいいのでしょうか?
図-12のように、幅 d の窓に光束が広がりながら入射する場合を考えます。そして平行光束が窓の法線に対してθ だけ傾いて入ってくるとします。
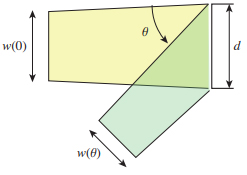
図 12: 窓に入射する光束
窓を通過できる光束の幅を w(θ) とすると

となることは幾何学的な計算からすぐわかります。つまり、窓に対して斜めの光束は窓を通過する光量が減ってしまう、ということです。逆に言えば同じ太さの光束でも斜めにしてやれば広い範囲を照明できるということで、その分単位面積あたりの光量は減る、ということです。
照明技術の言葉で言えば、物体表面の単位面積あたりに入射する光束の量を照度、il-luminance と言います。同じ強度の光束でも照明したい表面に斜めに入ると光束の量が減り、つまりはその分暗くなるのを考慮した量です。
照度の定義は厳密には、物理量ではなく目の波長あたりの感度で補正された量ですが、単一波長で絶対値を問わない場合は気にする必要はありません(なぜか照度に対応する物理量、例えば次元がW/m2 となるような量に名前はついていません)。
図-11のような光学系で「均一な照明」とするためには、この斜め入射の効果を考慮する必要があり、均一性の評価は「光の強度」ではなく「照度」でする必要があります。
さらに、平行光ではなく広がりながら進む光束では光源からの距離も影響することは直感的にわかります。
Lineman
他社の製品では以上で説明した光強度と照度の区別があいまいなまま仕様化されているものも見受けられますが、私たちの製品Lineman は原理的に厳密に定義/計算/設計され(図13)、そして評価されています。
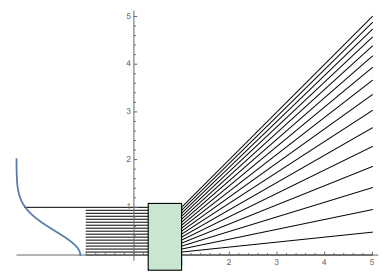
図 13
高い光線はほとんど 45 °方向に出て光線密度が上がっていることがわかります。これも実際の光学素子で実現するには非球面が必要となります。
レーザーの信頼性
半導体レーザの信頼性(バスタブ曲線、ワイブル分布、スクリーニング)
半導体レーザ製品の寿命はワイブルプロット、MTTF 及びスクリーニング等の技術用語表されることが多く、慣れていないと直感的に理解しにくいところがあります。本稿ではこれらの寿命や信頼性に関わる用語のバックグランドや意味を解説します。
半導体レーザに限りませんが、製品を使用するときの故障率の時間推移は次図のようになります。その形状からバスタブ曲線と言われています。
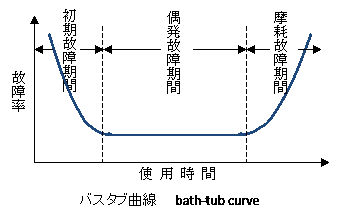
図 1 バスタブ曲線
製品の故障率は時間に対して一定ではなく以下の 3 つの領域に分類されます。
初期故障領域 :導入当初は部品の不良や調整の不良による故障が発生しますが、取替や修正により、時間とともに故障確率は減少します。
偶発故障領域 :初期故障がほとんどなくなると安定状態になります。しかし、偶発的な故障は発生しますので、故障率は一定の値になります。
摩耗故障領域 :長期間使用していると、部品の劣化が起こり、時間とともに故障が多くなります
このような一連の故障率の推移は、半導体レーザに限らず多種多様な分野で見られます。どの分野においても製品として好ましいのは生産が安定し初期不良が取り除かれた状態、つまり偶発故障期間のものの使用になります。
半導体レーザメーカーは、自社のレーザの初期不良が十分に取り除かれた状態であることを確認する必要があります。この確認作業で使用されるのがワイブル分布です。ワイブル分布は、上述の3つの故障確率を数式化するのに適した確率分布です。この分布を用いることよりバスタブ曲線を数学的に記述でき様々な分析や判定を行うことができます。
半導体レーザメーカーは自社での寿命試験、一般にエージング試験と言いますが、このエージング試験結果を累積故障率F(t)としてワイブル確立紙にプロットします。エージング試験は一般には最大動作保証温度で千時間オーダー行い、エージングカーブを外挿 して各々の故障時間推定します。累積故障率F(t)をワイブル確立紙にプロットするとこれから形状パラメータや時間パラメータが推定できます。推定された両パラメータから半導 体レーザの信頼性に関する情報を得ることが出来ます。具体的には下記の手順を参照して ください。
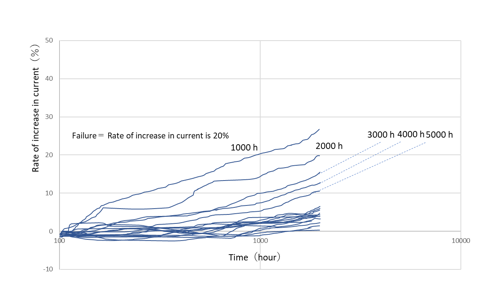
図 2 エージングカーブ
図 2 はN=30、2000h のエージングカーブ例です。縦軸は半導体レーザの動作電流の増加率です。一般にある一定の増加率に達すると故障とする例が多く、ここでは増加率 20%を故障と定義しています。5 個故障しており、1000,2000,3000,4000,5000h で 5 個が故障しています。(3000,4000,5000h はカーブを外挿しています)。この結果をワイブル確立紙にプロットしますと下図になります。
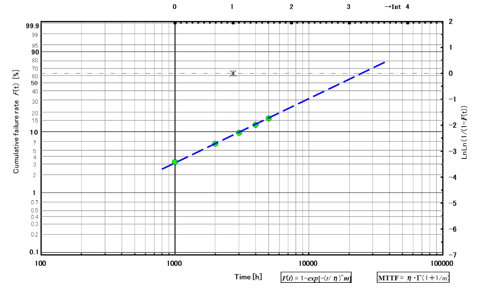
図 3 ワイブル確率紙
プロットしたF(t)の傾きからから形状パラメータ m 値を推定することができます。具体的には以下の手順です。
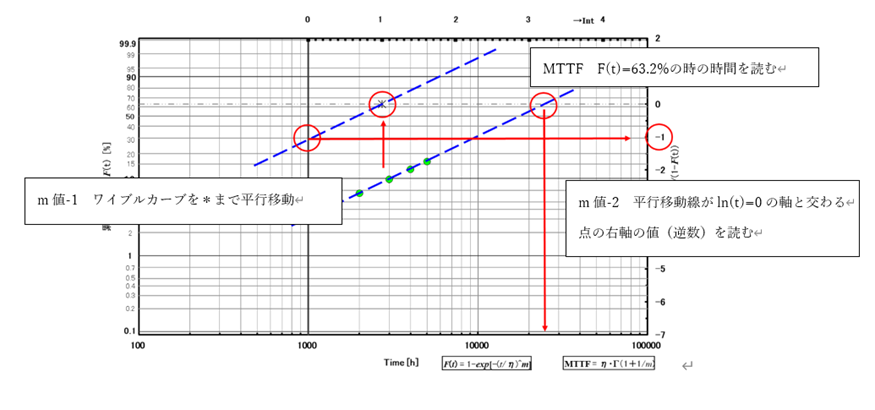
図4 ワイブル確率紙の使い方
m=1:時刻tに関係なく故障率λ(t)は一定になります。m=1は、この製品が偶発故障領域に属すると見ることができます。
0<m<1:故障率λ(t)は次第に緩やかになる右下がりの曲線になります。初期故障領域と見ることができます。
1<m:故障率λ(t)は次第に急になる右上がりの曲線で m 値が大になると急激に増大します。摩耗故障領域と見ることができます。
MTTFは、63.2%が故障する時間を示しています。 ワイブル確立紙にプロットした縦軸63.2%を与える時間が MTTF となります。このように半導体レーザメーカーは寿命試験を行いワイブル確立紙にプロットしたワイブルカーブを見ることで、自社の製品がバスタブ曲線のどの故障領域に位置するか、及び時間尺度の指標である MTTF の値を得ることができます。次にワイブル確立紙にプロットされたワイブルカーブの具体例を紹介します。
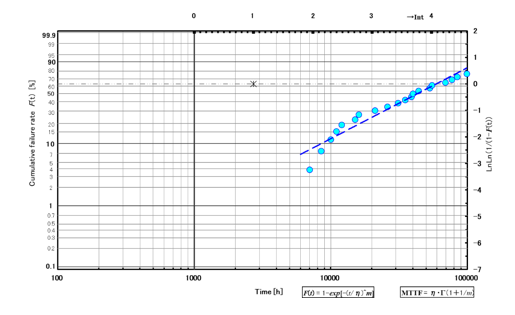
図 5 ワイブルカーブ 1
m=1.05、MTTF=60000h(N=25)です。この半導体レーザは偶発領域と考えられ、1000h付近の不良率も十分低く抑えられています。
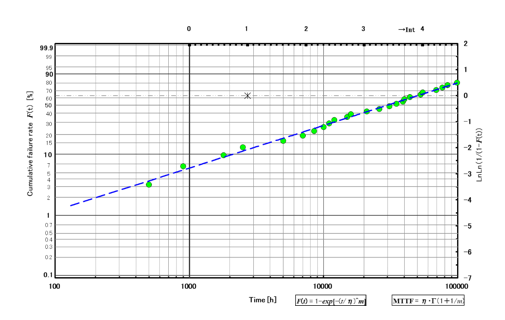
図 6 ワイブルカーブ 2
m=0.75、MTTF=50000h(N=30)です。MTTF は先例と比較して 10000h 程度の違いであるのに対し、1000h 付近の初期不良率が急減に悪化しています。この場合レーザメーカーはm=0.75 も含めて初期故障領域にあると判断し、次に述べる適切なスクリーニング手法を検討しなければなりません。
スクリーニングはレーザ製品が初期故障を含んでいる場合、これを選別し排除する手法 です。通常はレーザの静特性、例えば動作電流や閾値電流、光出力-電流カーブの微分効率などでの選別、あるいは短時間のエージングを行って初期劣化率で選別を行う等します。選別方法が明確でない場合はあらかじめ静特性値や初期劣化率付きのサンプルを長期エージ ングにかけ、ワイブルカーブを観測しながら有効な選別手段を決めていく必要があります。次図のようにスクリーニングによって初期不良 5 個をリジェクトしますと、ワイブルカーブは急速に改善する様子がわかります。
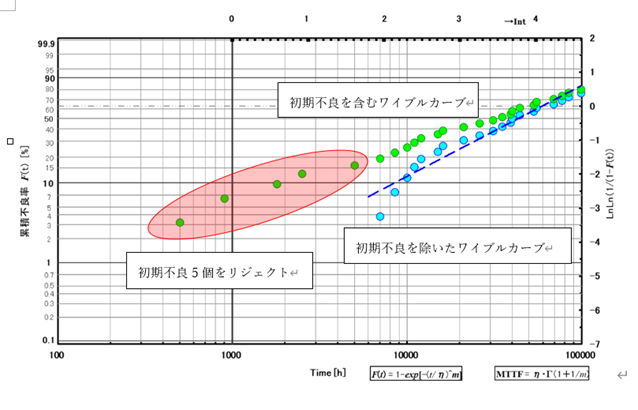
図 7 ワイブルカーブ 3
このようにワイブルカーブは半導体レーザの信頼性を確認するのに有効で広く利用されています。半導体レーザの採用を考える場合には、MTTF の値だけでなくワイブルカーブを入手し、その傾きや初期故障の有無を自社の製品信頼性仕様と照らして確認することが重要です。
精度を極める!【ラインマンレーザー&レンズ調整機】
ラインレーザーモジュール・LINEMANシリーズの特性及び品質の要となる半導体レーザーとレンズの微細な位置調整は、光学、電気、メカの専用設計が施された彩世オリジナルの調整機を用いて行われます。

彩世(あやせ)の光学技術者による論文(OPTIK掲載)
弊社の光学技術者が論文をOptikに投稿しました。論文の内容は以下の通りです。
- 単玉非球面レンズ2面の形状を数値積分で決定
- 球面収差とコマ収差が「完全に」補正されたレンズの面形状が瞬時で得られる
- 近軸量を初期データとして与えるだけ
- 同様の設計手法でトップハット変換レンズや、ベッセルビーム生成レンズなどが設計可能であることを証明
- Mathematicaで実行可能な設計ソフトを公開、ソフトはRaspberry Pi同梱のMathematicaでも実行可能
これまでカメラ用ズームレンズや顕微鏡対物レンズ、レーザ用のコリメータまで全てのレンズ設計はいわゆる「最適化」の手法で行われていました。これはコンピュータの上でレンズの光学的な特性をシミュレートして、必要な性能に達するまでカットアンドトライを繰り返すもので、どんな設計にも対応できますが、以下のような問題がありました。
- 過程によって結果が異なる
- 解があるかどうかやってみないとわからない
- いつ終わるかわからない
- 最終結果に「良い悪い」がつきまとう
- 設計者の経験と勘が必要
今回の論文では、
- 非球面を2面持つ
- 他に面が複数あってもよいが、固定されているものとする
- 回転対称である
- 光軸上から出る光線束のみ扱う
という制限の上で
- 近軸パラメータ(光軸付近のレンズパラメータ)を与える
- 数値積分によりふたつの非球面の形状を決定する
を行ってレンズ設計ができることを示しました。
論文のもとになっているのは70年以上前の1949年に出版されたWassermannとWolfによる「On the theory of aplanatic aspheric systems」という論文に出てくる方程式です。
この方法によると
- パラメータを決めると面が一意に決まる
- 面形状決定に要する時間がほぼ一定
- 与えたパラメータに対する解があるかどうかはそのパラメータだけで決まる
- 数値積分ができれば誰でもでき、誰でも同じ最良解に到達する
- パラメータが従来方法に比べて少ないので、パラメータ間の最適化も容易
という特徴があります。
ただし、上に述べた制限があるため、どんなレンズにもこの手法が使えるわけではありません。例えば撮像用のレンズなどで、いろいろな画角での特性をまんべんなく良くしたい、というような設計はできません。しかし、レーザコリメータや光ディスク用の対物レンズの設計にはこれまでのCodeVやZemaxなどの最適化ソフトウェアは、これでまったく必要なくなったと言えます。
また、論文内で示したように、トップハット変換レンズやベッセルビーム生成レンズなど「結像しないレンズ」も設計可能となります。これ以外にもいろいろな応用が考えられます。
しかも高いハードウェアパフォーマンスが不要で、Raspberry Piで実行可能です。例えば、専門家でも苦労するBlu-ray用対物レンズ等は、容易に設計可能です。下図のような設計が1秒以下でできます。興味のある方は是非試してみてください。



